For GAMES WITH OPPONENTS AS SEARCH

• The minmax algorithm is designed to determine the optimal strategy for MAX and to suggest, therefore, the first best move to be performed;

• MIN is assumed to play at opposite‘s best

• We are not interested in the path but only in the next move

• Complete? Yes (if the tree is finite)

• Optimal? Yes (against an opponent who plays at his/her best)

• Temporal complexity? O(bm)

• Space complexity? O(bm) (depth-first)

  • For chess, b ≈ 35, m ≈100 for "reasonable" games

Alpha-Beta Cuts

• Consider a node N in the tree. Will the player move to that node?
• If the player had a better choice (we call it M) in the parent node level or at any point along the path, then N will never be selected. If we reach this conclusion we can eliminate N.
• Call ALFA the value of the best choice found on the path for MAX (the highest) and BETA the value of the best choice found on the path for MIN (the lowest).
• The algorithm updates ALPHA and BETA and cuts branches when their choice the worst.
• Example：
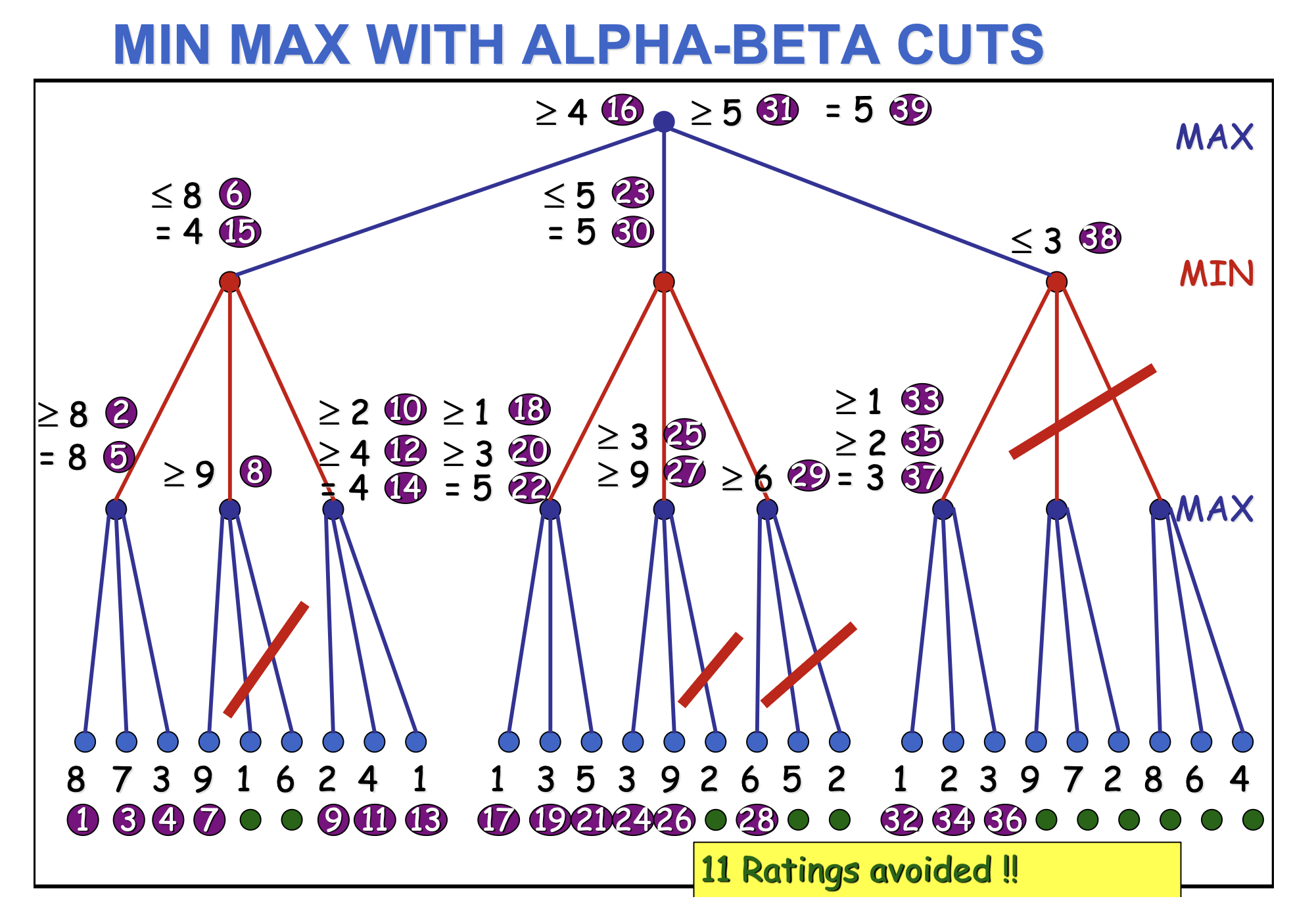
  • 分别写出$\alpha =-\mathrm{\infty },v,\beta =\mathrm{\infty }$ ，这三个数字应当是从小到大（$\alpha \le v\le \beta$），否则右子树会被裁掉。在MAX节点考虑$\alpha \le v$, 在MIN节点考虑$v\le \beta$.

EFFECTIVENESS OF CUTS

• Obviously if you always evaluate the worst nodes, then best nodes are always in the search path and there is no cut.
• The best case is when the best nodes are evaluated first. The other are always cut (of course it is entirely theoretical).
• In this case we can reduce the number of nodes (which is bd) to about bd / 2. (In practice, it is reduced by the square root branching factor, or you can look forward twice more at the same time).
• In the average case with random